Bevezetés:
Az Interneten böngészve láttam, hogy hobby szinten sokakat érdekelnek a csöves áramkörök, elsősorban a hangerősítők. Építenek, felújítanak, különböző megoldásokat is kipróbálnak; számos vita zajlik a csöves hangzást illetően - melyik a legjobb? Rengeteg mitikus hit terjed; az „igazi hangzáshoz" aranyozott kábelek, olajpapír kondenzátorok, szénréteg ellenállások és ki tudja még mik kellenek. Ha csak a „csöves hangzás” okát keressük, el kell tekintünk a kondenzátorok, ellenállások, kábelek, kimenő trafók, stb. hatásától. Cikkemben ezt teszem, bemutatom mi a „csöves hangzás” specifikus oka:
Egy vákuumcső izzó katódja körül kialakuló tértöltés valamennyi elektroncső sajátossága. Nyilvánvalónak tűnt, hogy a csöves hangzást ez okozza. Feltettem magamnak a kérdést: létezik e olyan általános megoldás, amely az erősítés (hangerő) érdemi megváltoztatása nélkül képes a tértöltés-hatás (a csöves hangzás) mértékének a változtatására.? A válaszom igen. Felállítottam egy elméleti matematikai modellt, majd a gyakorlatban mérésekkel ellenőriztem, és megállapítottam, hogy helyesen írja le a valóságot. „A puding próbája az evés" - terveztem és készítettem egy elektronikus készüléket, amivel a tértöltés-hatás nagyságát (a „csöves hangzást") szabályozható módon változtatni tudom egy erősítőben.
A tértöltés hatása az elektroncsövek működésére:
Az 1960-as évekre az elektroncsövek tervezéséhez és felhasználásukhoz szükséges elméleti és gyakorlati ismeretek kialakultak és bárki számára elérhetővé váltak [1, 2, 3, 4]. Akit az elektroncsövek konstrukciós háttere és működési törvényszerűségeik részletei érdekelnek, azoknak érdemes a hivatkozott irodalmat tanulmányozni.
A dióda:
Tértöltés modulátoromhoz egy 6Х2П (latin átírásban: 6H2P) típusú kettős diódát használtam: hét lábú, miniatűr elektroncső és két darab egymástól független hengeres diódát tartalmaz. Fotója az 1. ábrán, karakterisztikája [4] pedig a 2. ábrán látható.
 1. ábra 6H2P dióda | 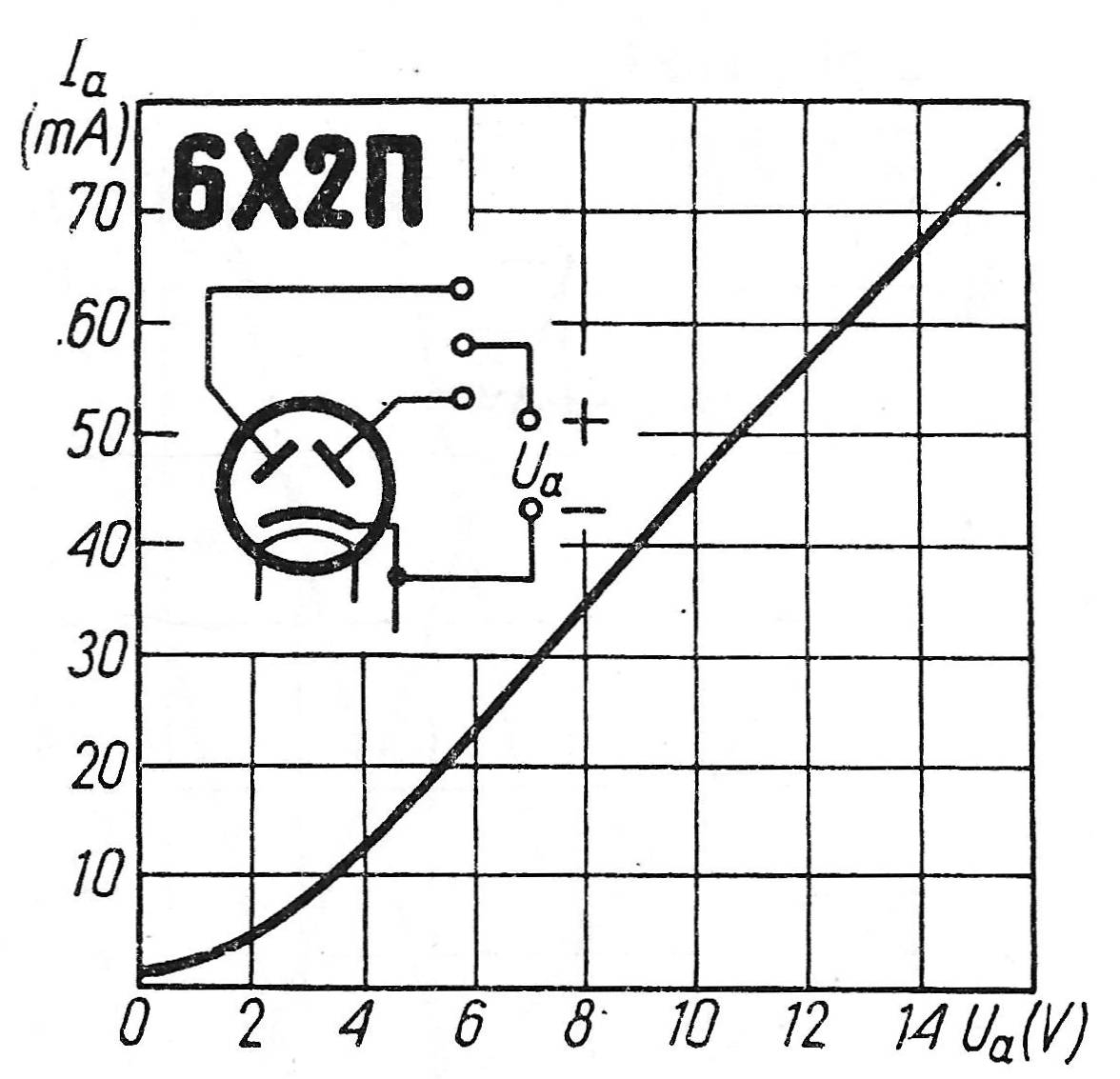 2. ábra 6H2P dióda karakterisztikája |
Mint látható, nulla anódfeszültségnél is folyik áram: ezt induló áramnak nevezzük. Ha egy nagy belső ellenállású feszültségmérővel megmérjük az anód-katód feszültséget, azt tapasztaljuk, hogy az anód nagyjából egy volttal negatívabb a katódnál. Az izzó katódból spontán kilépő termikus elektronok feltöltik az anódot. A katód és az anód közötti vákuumtérben lévő elektronfelhőt tértöltésnek nevezzük.
Ha a csőre feszültséget kapcsolunk és az elektródák ekvipotenciálisak (saját belső ellenállásuk elhanyagolhatóan kicsi), a csőben kialakuló elektromos térerősség-eloszlást a tértöltés, a belső geometriai jellemzők és a rákapcsolt feszültség nagysága szabja meg.
Henger- és síkdiódák esetében az áram-feszültség függvény azonos alakú:
IA = P·UAK3/2.
Az anódáram, az anód-katód feszültség 3/2-ik hatványával arányosan nő. A "P" arányossági tényező, az úgynevezett perveancia csak a cső geometriájának a függvénye, azaz állandó.
Ha figyelmesen megnézzük a 2. ábrát, ránézésre látjuk, hogy a hatványfüggvény jelleg csak a görbe első harmadára lehet igaz: 10V-nál nagyobb anódfeszültségnél az Ia - Ua függvény egyre lineárisabbá válik. Ennek oka az oxidkatód belső ellenállásának növekedése. (Az ábrán nem látható, de meg kell említeni, hogy a feszültséget tovább növelve, az áram egyre lassabban nő, majd állandóvá válik. Ez az úgynevezett telítési szakasz.)
Felmerült bennem a kérdés: mennyire követi a valóság az elméletet? Felnagyítottam a 6Х2П karakterisztika ábrát úgy, hogy 1mA áramerősség 2mm hossznak feleljen meg, majd 2, 4, és 6 voltnál vonalzóval lemértem az áramerősség értékeket. Végül ezekre a pontokra - az alapegyenletből - kiszámítottam P értékét és eredményül: 1,59; 1,56 és 1,56 mA/V3/2 értékeket kaptam.
Az eredmény meggyőzött arról, hogy ez a dióda valóban henger kivitelű és követi az elméletet, mert P értéke - a csekély szórástól eltekintve - állandónak bizonyult.
A trióda:
A henger- és síktriódák katódáramát kétváltozós függvény írja le:
IK = P·(UGK+(UAK/μ+))3/2.
P - pervencia csőállandó, amit az adott trióda geometriai paraméterei határoznak meg.
μ+ - csőállandó, amit statikus erősítési tényezőnek nevezünk.
IK értéke akkor válik nullává, ha a zárójeles kifejezés értéke éppen nulla. Így μ+ értékének meghatározásához a karakterisztikában megkeressük azt a pontot, amikor a negatív rácsfeszültség a csövet éppen lezárja. Ebben a pontban μ+ = -UAK/UGK értékével.
Nézzünk meg egy konkrét példát a csőállandók meghatározására. Használjuk fel ehhez egy novál kettőstrióda 6Н6П (latin átírás: 6N6P) adatait. A cső fotója a 3. ábrán, karakterisztikái pedig a 4. és 5. ábrán láthatók.
 3. ábra 6N6P trióda | 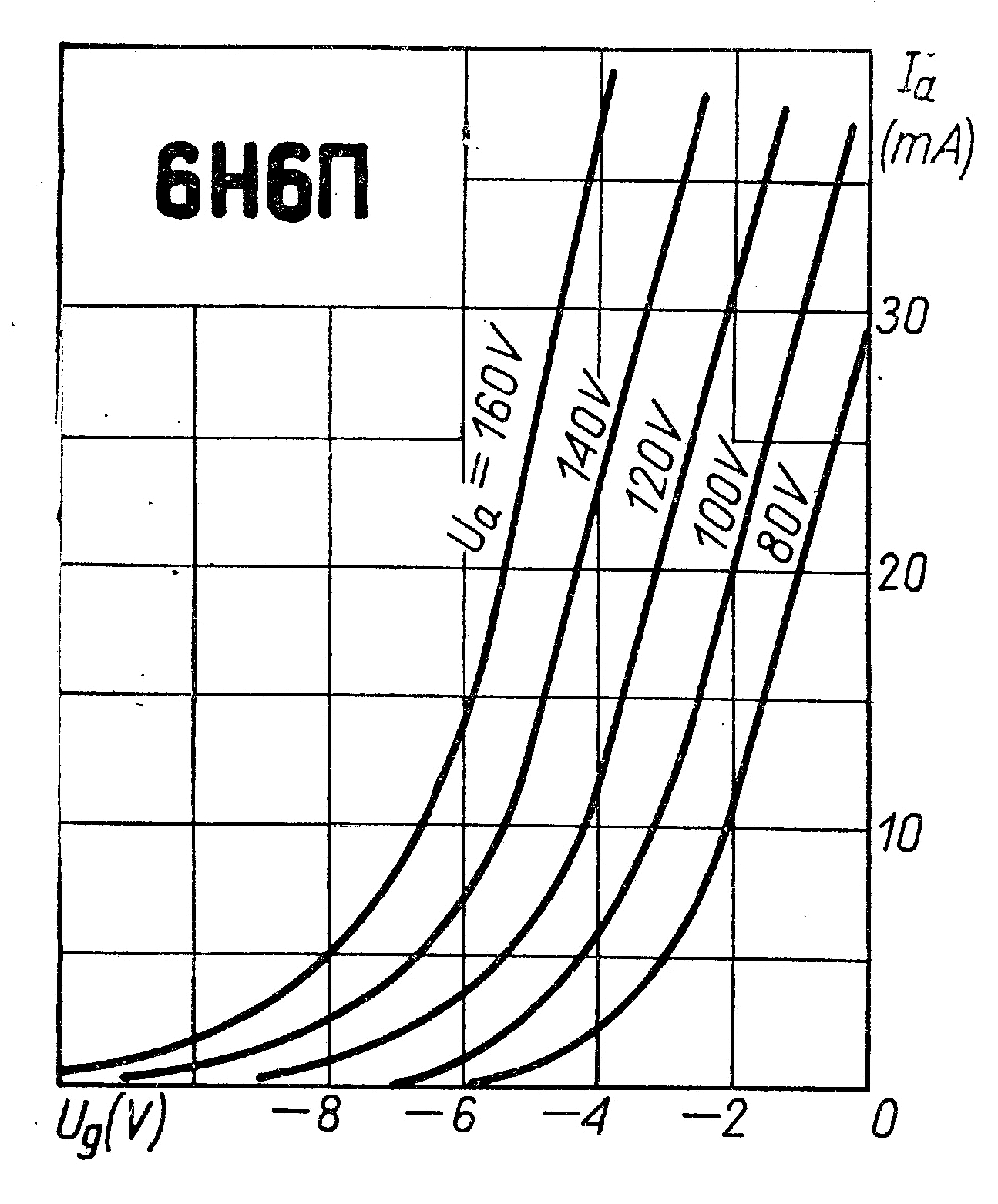 4. ábra 6N6P trióda karakterisztikája | 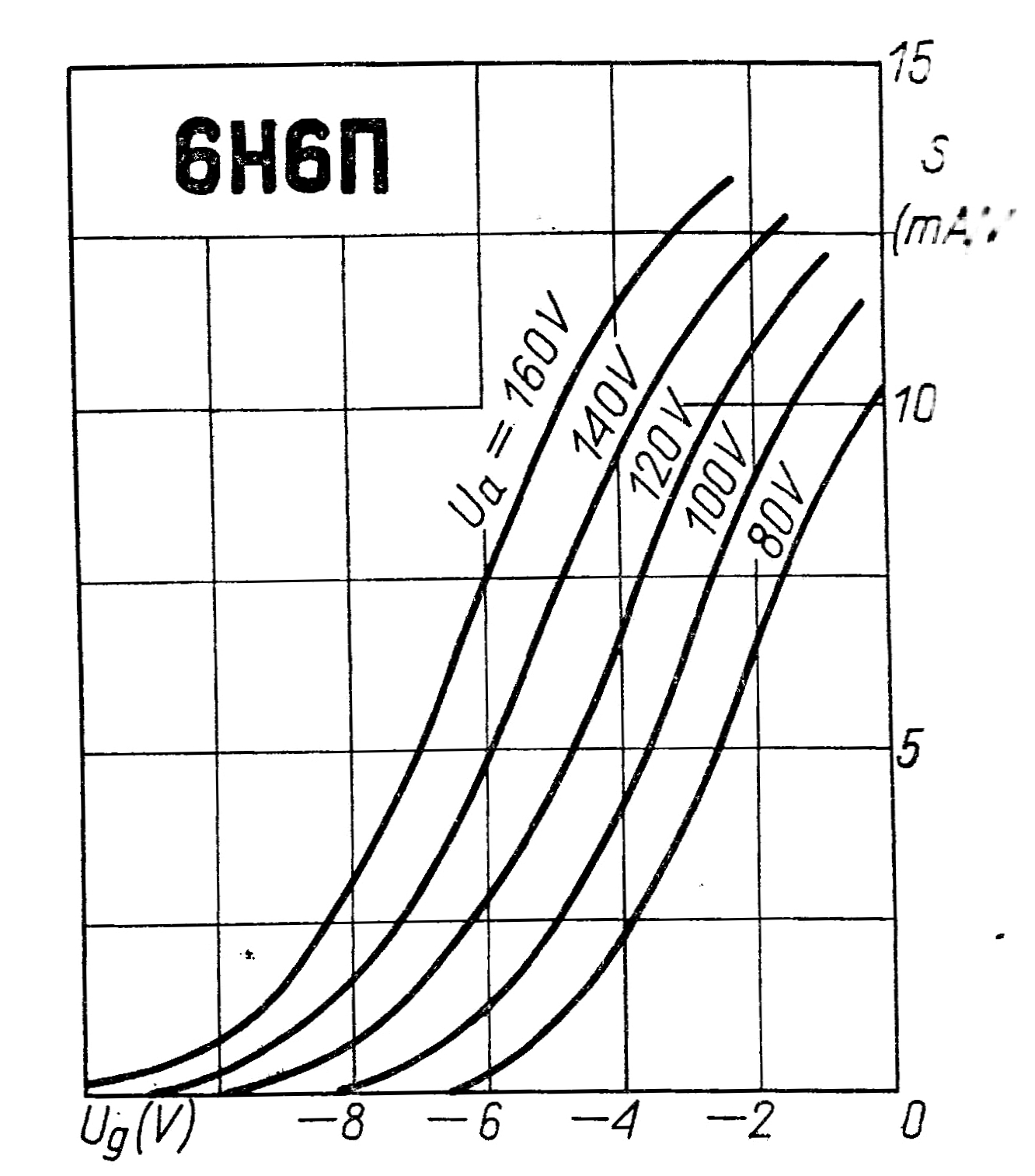 5. ábra 6N6P trióda karakterisztikája |
Jól látszik, hogy az Ug-Ia karakterisztika (4. ábra) exponenciális jellegű, és a cső meredekség változása is (5. ábra) erős nemlinaritást mutat. A 4. ábra és a fentiek alapján meghatároztam a csőállandókat: μ+ = 13,3 és P = 1,14 mA/V3/2
A pentóda:
Az elektroncsövek fejlesztésének egyik célja a minél kisebb torzítás elérése volt. Ezt a célt többrácsos csövekkel lehetett elérni. A pentódák működését már nem lehet egyetlen analitikus függvénnyel leírni, az üzemi tartományban a csövön folyó áram nagyrészt a rács-katód feszültségtől függ. Példaként vizsgáljuk meg az EF80 típusú pentódát: fotója a 6. ábrán, jellemző karakterisztikái pedig a 7. és 8. ábrán láthatók.
 6. ábra Az EF80 pentóda | 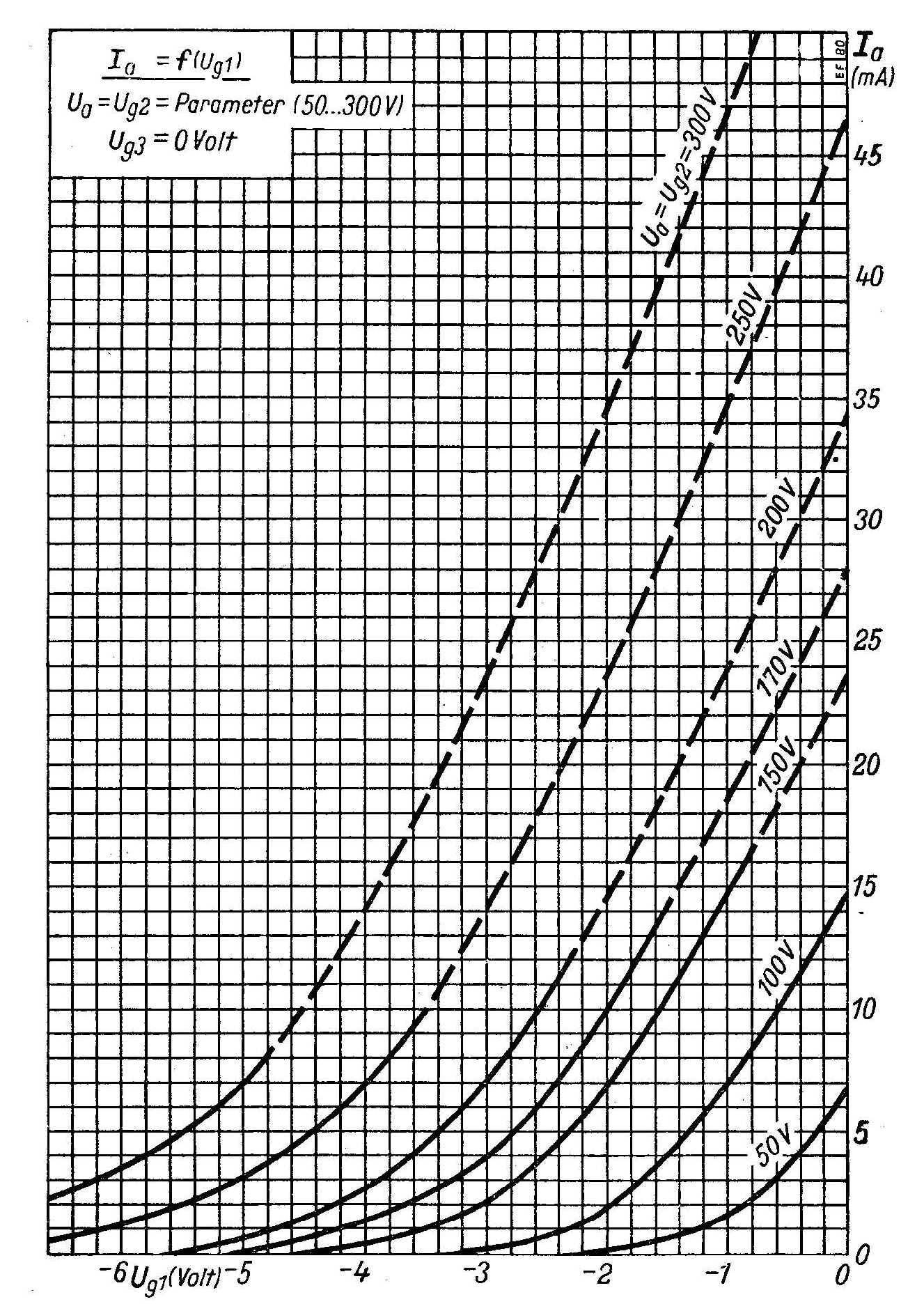 7. ábra Az EF80 pentóda karakterisztikája | 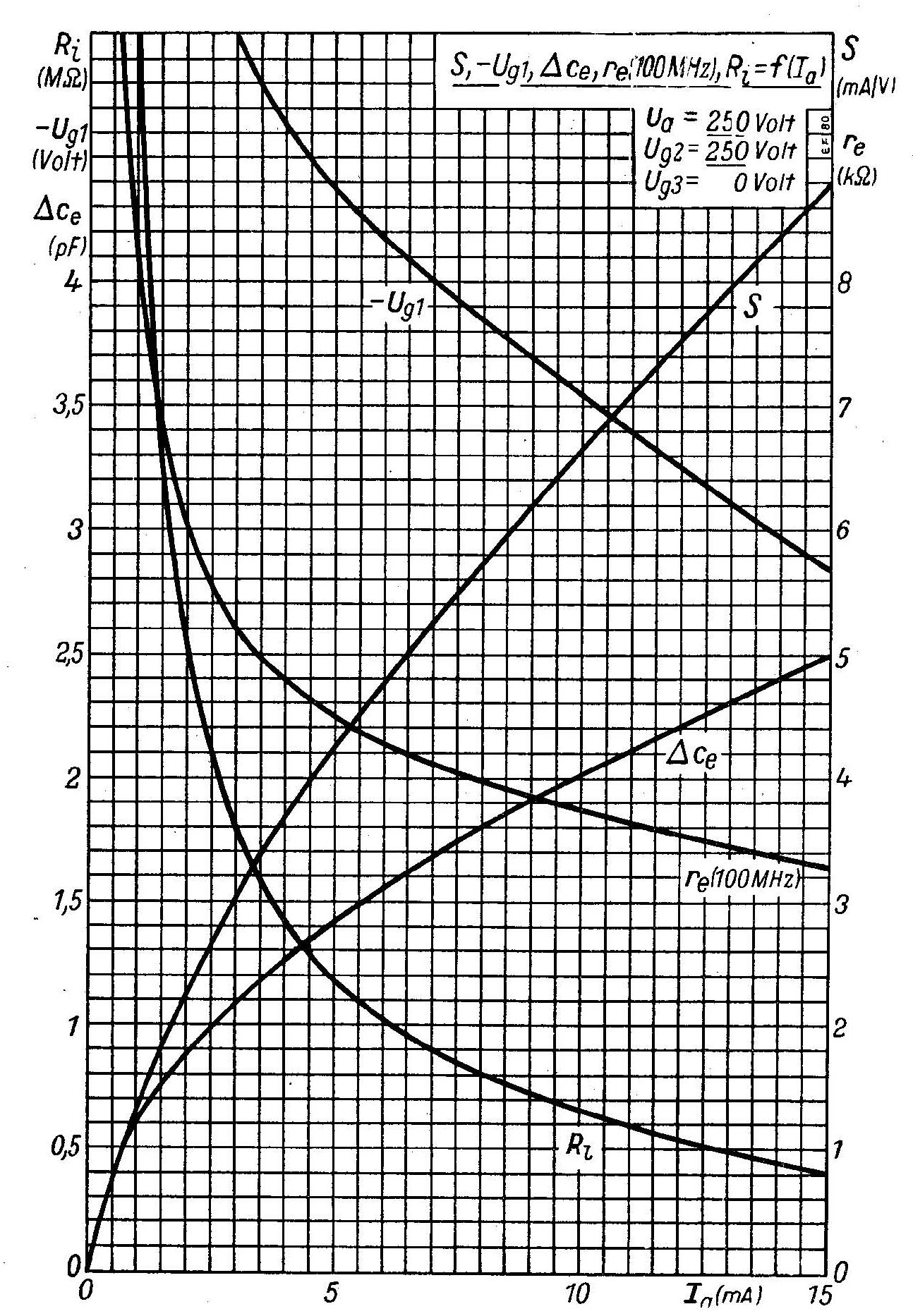 8. ábra Az EF80 pentóda karakterisztikája |
Ránézésre is látszik, hogy az anódáram függése az anód- és rácsfeszültségtől csaknem lineáris. Megfelelően visszacsatolt pentódás fokozatokkal tehát jó lineáris hangerősítők készíthetők: eltűnik a "csöves" hangzás. Nem véletlen, hogy az audiofil csöves erősítőkben mindíg találunk triódát.
A kellemes csöves hangzás mértéke és mérése:
A '"kellemesség" mindig szubjektív dolog. Ha egy audiofil erősítőt hallgatunk és a hangzást kellemesnek találjuk, hogy állapítsuk meg ennek a mértékét? Nyilvánvaló, hogy torzítás okozza a hatást. Próbálkozzunk torzításmérővel? Aligha. A hagyományos torzításmérők azt mutatják meg, hogy egy mérési frekvencián hány százalék a felharmonikusok összegzett effektív értékének és az alapharmonikus effektív értékének az aránya. Azt nem fogjuk megtudni, hogy a felharmonikusok amplitúdó eloszlása milyen. Próbálkozhatunk spektrum-analizátorral, de a látott kép kiértékelése nem igazán egyszerű.
A legegyszerűbbnek számomra az tűnt, ha feszültségméréssel pontonként kimérem a kimeneti feszültség változását a bemeneti feszültség függvényében Uki=f(Ube). Azt vártam, hogy a kimeneti feszültség, illetve annak változása egy lineáris és egy háromkettedes hatványfüggvény összegeként felírható lesz.
A méréshez kellett találnom egy olyan erősítő kapcsolást, amelyet a csöves hangzás kedvelőinek többsége preferál: Ágoston Lajos "Hibrid erősítők" című cikke (Rádiótechnika 15/7-8.) alapján a 6N6P csöves SRPP áramkört választottam.
A 9. ábrán láthatjuk a vizsgált áramkör elvi rajzát, a mérés gyakorlati kivitele pedig a 10. ábrán látható.
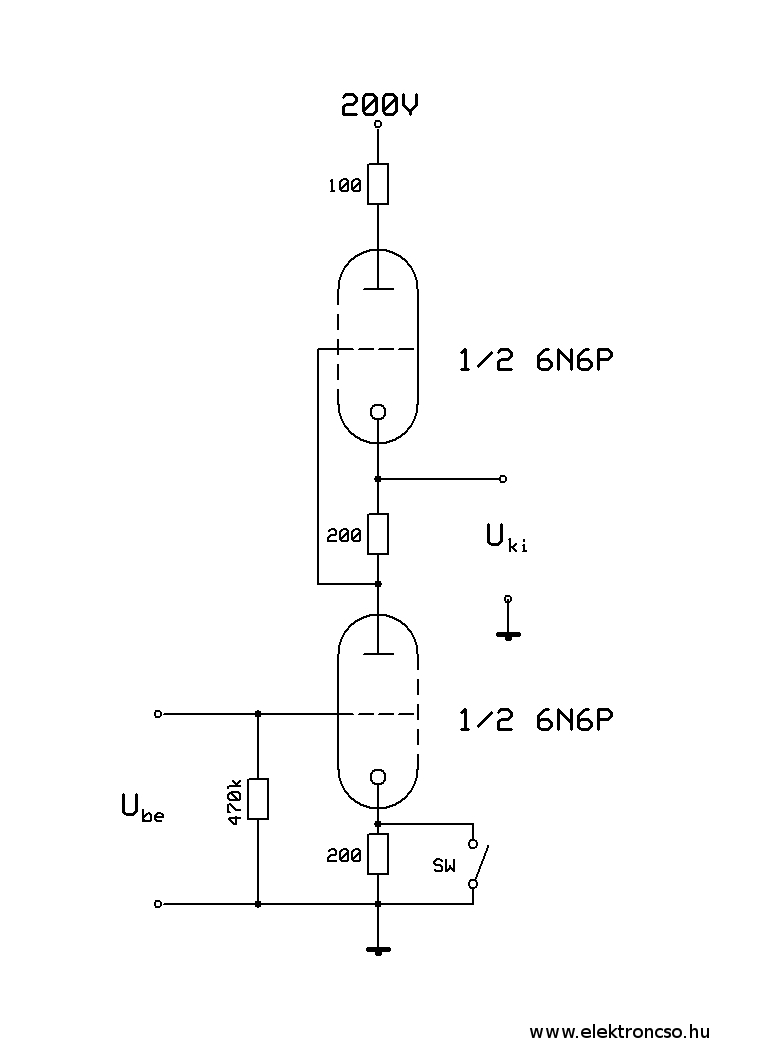 9. ábra A 6N6P csöves SRPP áramkör |  10. ábra A 6N6P csöves SRPP áramkör gyakorlati kivitele |
Az ellenállásokat egy novál csőfoglalat lábaihoz forrasztottam, majd a teljes áramkört aranyozott tüskékkel csatlakoztattam a csőmérőmhöz. A csőmérőm biztosította a fűtőfeszültséget, a 200V-ot és a bemeneti rácsfeszültséget is. Az Uki feszültséget digitális multiméterrel mértem. Legelőször az SW kapcsoló nyitott állásában megmértem az alsó csőfél munkaponti rácsfeszültségét, ami pontosan -2,50V értékűnek adódott. Majd a kapcsoló zárt állása mellett, a bemeneti feszültséget -1,5V és -3,5V között, tizedvoltos lépésekben változtattam és megmértem a kimeneti feszültségértékeket.
A mérési eredmények az 1. számú táblázatban olvashatók (∆Uki az egymást követő kimeneti feszültségértékek különbsége):
1. táblázat
| -Ube [V] | Uki [V] | ∆Uki [V] |
| 1,5 | 83,76 | 0 |
| 1,6 | 85,01 | 1,25 |
| 1,7 | 86,26 | 1,25 |
| 1,8 | 87,72 | 1,46 |
| 1,9 | 88,88 | 1,16 |
| 2,0 | 90,23 | 1,35 |
| 2,1 | 91,49 | 1,26 |
| 2,2 | 92,74 | 1,25 |
| 2,3 | 94,00 | 1,26 |
| 2,4 | 95,26 | 1,26 |
| 2,5 | 96,70 | 1,44 |
| 2,6 | 97,59 | 0,89 |
| 2,7 | 98,74 | 1,15 |
| 2,8 | 100,01 | 1,36 |
| 2,9 | 101,26 | 1,16 |
| 3,0 | 102,41 | 1,15 |
| 3,1 | 103,57 | 1,16 |
| 3,2 | 104,73 | 1,16 |
| 3,3 | 106,09 | 1,36 |
| 3,4 | 107,15 | 1,06 |
| 3,5 | 108,31 | 1,16 |
Az Uki=f(-Ube) függvény kissé nemlineáris. Lineárisan legjobban az Uki=83,76+12,5·(-∆Ube) egyenes szakasszal közelíthető. A 11. ábrán látható a mért értékek és a hozzá illeszkedő egyenes ábrája. A piros pöttyök a mért értékeket, a zöld keresztek pedig az egyes pöttyökhöz tartozó egyenes megfelelő pontjait jelölik.
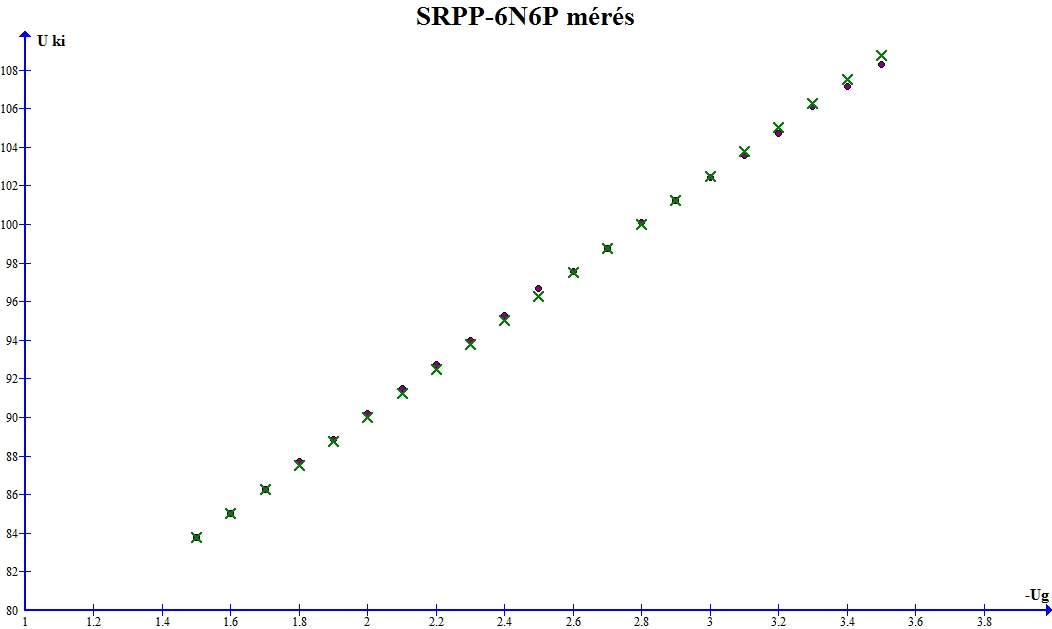 11. ábra Az 1. táblázat mérési eredményei ábrázolva és a hozzá illeszkedő egyenes ábrája.
Tudjuk, hogy a linearitás hibát a tértöltés okozza. Ha a tértöltés hatásának megfelelően úgy görbítjük meg az egyenes szakaszt, hogy a végpontja egybeessen a mért függvény végpontjával, meghatározhatjuk a tértöltés-függésnek az erősítésben betöltött súlyát:
Az egyenes szakasz Uki végpontja: 108,76V
A mért függvény Uki végpontja: 108.31V
Tehát a tértöltés okozta kimeneti feszültségváltozás: -0,45V
UkiMAX - UkiMIN = 24,55V
Az adatokkal felírt egyenlet: w·24,553/2 = 0,45
Ebből a tértöltés súlya: w = 0,0037, azaz 0,37%
Tértöltés modulátor:
Elméletemre alapozva terveztem és készítettem egy olyan készüléket, amellyel a tértöltés-hatás súlya egy erősítő rendszerben széles határok között beállítható, azaz a "csöves hangzás" az egyéni ízléshez igazítható. Ezt a szerkezetet tértöltés modulátornak (space charge modulator) neveztem el. Nem korrekt az elnevezés, de jobb híján megteszi: tehát nem a tértöltést modulálom, hanem a tértöltés hatással modulálok egy lineáris hangfrekvenciás erősítőt. Kapcsolási rajza a 12. ábrán, fotói pedig a 13. és 14. ábrán láthatók.
 12. ábra A tértöltés modulátor kapcsolási rajza
A készülék sztereo erősítő láncba köthető. Kétcsatornás, csatornánkénti erősítése egyszeres, tipikus bemeneti jelszint 0dBV. A tértöltés-moduláció súlya - az előlapi potméterekkel - mint additív tag beállítható, és az így módosított jel kerül a kimenetekre.
 13. ábra A készülék kivitele |  14. ábra A készülék oldalnézetből |
Két készüléket készítettem. Az egyiket zenehallgatásra (a tértöltés-hatás súlya 0-2% között változtatható; P1=P2=50kohm, R6=R15=1Mohm), a másikat gitártorzítónak (a tértöltés-hatás súlya 0-20% között változtatható; P1=P2=5kohm, R6=R15=4,7kohm).
A készülék két csatornája azonos kapcsolású, a működést a ch1 csatorna alapján mutatom be: a hangfrekvenciás jel "ac" csatoltan kerül az IC1 (3) nem invertáló bemenetére. A bemeneti fokozat egyszeres erősítésű. A bemeneti ellenállás (R1) 47kohm, a fokozat kimeneti ellenállása gyakorlatilag nulla. A kimenet IC1 (1) két ágra oszlik: az egyik ág a T1 tranzisztorból és az R3,R4,R5 ellenállásokból felépített áramgenerátor. Ez nem más , mint egy feszültség-áram konverter: a tranzisztor kollektorárama a bemeneti hangfrekvenciás feszültségváltozással arányosan változik. Ez az áram átfolyik a V1 vákuumdiódán. A dióda anódfeszültsége a tértöltés törvénynek megfelelően változik. Ez a váltófeszültség a C4 kondenzátoron, a P1 potenciométeren és az R6 ellenálláson keresztül, az IC1 második erősítőjének (6) invertáló bemenetére jut, ahol hozzáadódik az R7 ellenálláson keresztül érkező torzítatlan hangfrekvenciás jelhez. Az IC1 (7) kimenetén megjelenő Uout feszültség:
Uout = Uin + w·Uin3/2
tértöltés-hatás formulának megfelelő lesz. A dióda jellemzőin túlmenően a w súlytényező értékét a P1 potméter értéke és állása, valamint az R6 értéke határozza meg.
Az elektronika alapvetően felületszerelt kivitelben, egy 145x110 mm-es kétoldalasan folirozott panelen (15. ábra) foglal helyet. Néhány furatszerelt alkatrész van csupán: a csőfoglalat, a fűtőfeszültséget szolgáltató 2,4 W-os transzformátor, a ±12 V-os tápfeszültséget biztosító 1,8 W-os transzformátorok és az elektrolit puffer-kondenzátorok. Az áramkört egy P16C típusú dobozba helyeztem el. A doboz oldalára szerelt potméterek, be-kimeneti RCA csatlakozók és a hálózati kábel is bontható módon csatlakozik a panelhez.
Néhány mért adat (jellemző értékek):
Bemenő jel nélkül: V1 anódáram: 12,4-13mA
V1 anódfeszültség: 4,16-4,4V
U out offset feszültség < ±1mV
Uin = 1kHz 2Vpp négyszögjel esetén: V1 anódfeszültség váltó komponense: 215-230 mVpp
 15. ábra A tértöltés modulátor nyákterve
Ha valaki szeretné e készüléket kipróbálni, szívesen kölcsönadom. Ha netán megépíteni szeretné, a panelgyártáshoz szükséges GERBER fájlokat díjmentesen megküldöm.
A hangok spektruma:
Szerettem volna tudni, milyen hatást gyakorol egy hangfrekvenciás jelre a tértöltés moduláció. Összeállítottam egy mérést. A gitártorzítónak szánt tértöltés modulátorom egyik csatorna-bemenetére 300Hz-es, 0dB nagyságú háromszög jelet adtam, és megmértem a kimenet frekvenciaspektrumát moduláció nélkül és maximális tértöltés modulációnál (w ≈ 0,2) is.
A méréshez a Velleman cég által gyártott PCSU200 típusú PC oszcilloszkópot használtam. Ez a készülék több funkcióval rendelkezik, többek között spektrum-analizátorként is használható. Nagy előnye, hogy az ernyőképek grafikus fájlként is tárolhatók, így e cikkbe is könnyű beilleszteni ezeket.
A 300Hz-es jel oszcilloszkópos képe a 16. ábrán látható. Nincs értelme erről két képet feltennem, mert a modulálatlan és a modulált jel első ránézésre azonosnak tűnik. Csak figyelmesen megnézve látunk némi különbséget.
 15. ábra A 300Hz-es jel oszcilloszkópos képe
A vízszintes tengelyen az idő (1ms/osztás), a függőleges tengelyen a feszültség (0,3V/osztás)
A 17. ábrán ennek a jelnek a frekvenciaspektrumát látjuk, a 18. ábrán pedig a tértöltés modulált jel spektrumát.
A vízszintes tengelyen a frekvencia: 0-3,9kHz (300Hz/osztás), a függőleges tengelyen a feszültség logaritmikus értéke (10dBV/osztás)
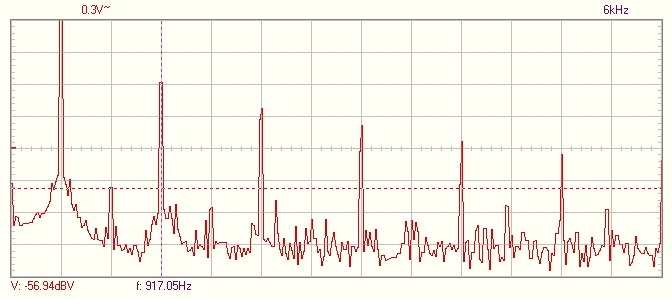 17. ábra A 16. ábra jelének frekvenciaspektruma
18_ábra
A vízszintes tengelyen a frekvencia: 0-3,9kHz (300Hz/osztás), a függőleges tengelyen a feszültség logaritmikus értéke (10dBV/osztás)
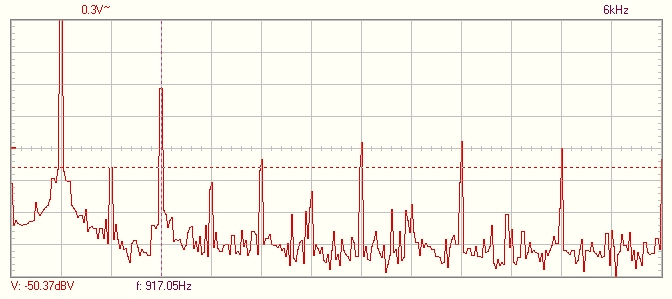 15. ábra A tértöltés modulált jel spektruma
Egy ideális háromszög jel Fourier spektruma csak páratlan felharmonikusokat tartalmaz. Ha az alapharmonikus amplitúdóját egynek vesszük, a felharmonikusok egymást követő amplitúdó értékei: f(3) = 1/ 32, f(5) = 1/52, f(7) = 1/72 nagyságúak, és így tovább...
A 17. ábrán látszik, hogy van egy kis torzulás: megjelentek páros felharmonikusok is. A második felharmonikus amplitúdója: -56,94dBV. A -60dB-nél kisebb amplitúdójú jeleket célszerű figyelmen kívül hagynunk, mert a zaj hatása jelentős.
A két ábrát összehasonlítva látjuk, hogy a tértöltés moduláció létrehozza, illetve jelentősen megnöveli a páros felharmonikus tartalmat, ugyanakkor csökkentve a páratlan felharmonikusok nagyságát. Összegezve; a frekvenciaspektrumot páros felharmonikusokban gazdaggá teszi, és ezt "bársonyosabb", "melegebb" hangzásként szoktuk értékelni.
| | |

